Tag: Compound Interest

The Power of Compounding Interest

Compounding interest is one of the core principles of long term investing. The basic is the more often your investment compounds, the greater your investment will become, and your investments will grow at a faster rate over time.

Compounding interest is also one of the basic ideas of the phrase “It’s about time in the market, not timing the market” — over time, as your investments compound interest, you will see greater and greater accelerated gains.

What is Compounding Interest?

Compound interest is interest added to the principal of a deposit or loan, so that the added interest also earns interest from then on. This addition of interest to the principal is called compounding.

To put this more simply, compound interest is “interest on interest” which means your deposit will grow at a faster rate than with simple interest.

Compounding Interest Formulas

Here are two formulas you can use to calculate compounding interest yourself.

Basic formula — for compounding once per year:

V = P (1 + r)^t

Where:
V = the value of investment at the end of the time period
P = the principal amount (the initial amount invested)
r = the annual interest rate (note: this is a decimal, so 5% becomes 0.05)
t = the number of years the money is invested
^ means raise to the power of

Example for compounding $1 initial investment at 5% over 50 years:

V = 1*(1+0.05)^50
V = 11.467

Advanced formula — for compounding multiple times per year, such as daily, monthly, or quarterly:

V = P ( 1 + [ r / n ] ) ^ n * t

Where:
V = the value of investment at the end of the time period
P = the principal amount (the initial amount invested)
r = the annual interest rate (note: this is a decimal, so 5% becomes 0.05)
n = the annual frequency of compounding (how many times a year interest is added)
t = the number of years the money is invested
^ means raise to the power of

Example for compounding $1 initial investment at 5% compounding monthly over 50 years:

V = 1*(1+0.05/12)^(12*50)
V = 12.119

Important: Notice how compounding more often per year yields higher returns.

Example of Compounding Interest

Here’s a quick example of compound interest:

You have invested $1 at a 5% interest rate which compounds once per year.

• Next year, the $1 investment would be worth $1.05 — a gain of $0.05.
• In 2 years, the initial $1 investment would be worth $1.1025 — a gain of $0.0525 over the previous year
• In 3 years, the initial $1 investment would be worth $1.158 — a gain of $0.0555 over the previous year.
• In 10 years, the initial $1 investment would be worth $1.623 — a total gain of $0.623.
• In 20 years, the initial $1 investment would be worth $2.653 — a total gain of $1.653.
• In 50 years, the initial $1 investment would be worth $11.467 — a total gain of $10.467!

Important: Notice how the gains are increasing year over year and accelerating!

Compounding Interest Over Time

Here are two graphs that further demonstrate the power of compounding interest.

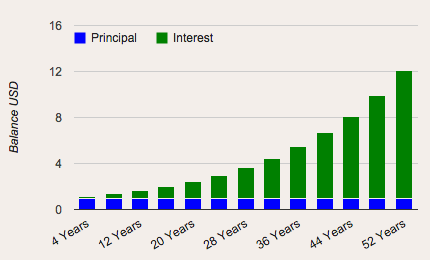
The first graph shows compounding interest of $1 initial investment and a 5% return rate over a 52 year period:

The next graph shows the compounding interest power of the same $1 initial investment and 5% return rate but over a 104 year period:

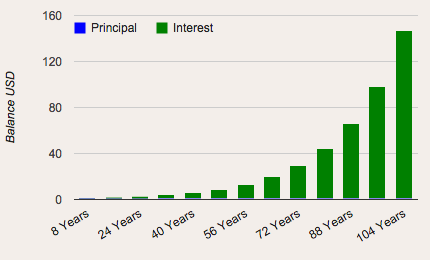
These graphs demonstrate the accelerating return rate you receive with compounding interest. The interest you’re making on your initial $1 investment is making its own interest — and it’s making more and more money over time — accelerating the returns.

Visual example of compounding frequency differences

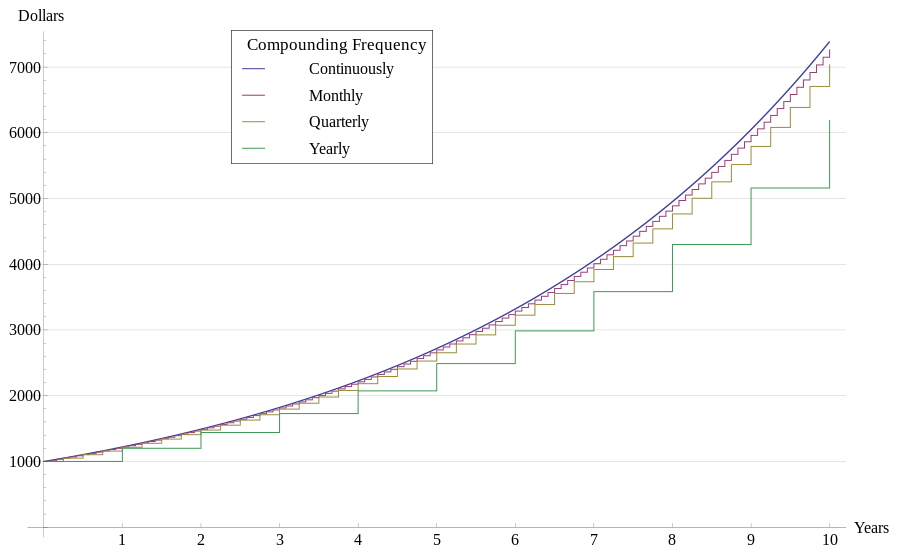
In this graph you will see compounding more often yields higher returns. Over time, the $1000 initial investment compounding yearly will return significantly less than $1000 compounding quarterly or monthly.

Takeaway: Interest compounding more frequently will ultimately yield greater returns.

Learn More about Compounding Interest

If you’d like to learn more about compounding interest and it’s benefits on investing, I’d recommend these three books:

The Richest Man in Babylon

The Compound Effect

A Beginner’s Guide to Investing: How to Grow Your Money the Smart and Easy Way